Solution: Horizontal Curves Set 1
Problem (1)
Given the following information:
Compute the curve components, endpoint stations, and radial deflections to full stations.
Curve components
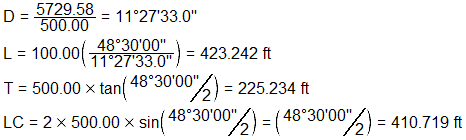
Endpoint stationing
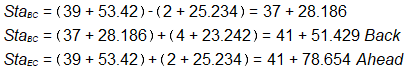
Radial deflection equations
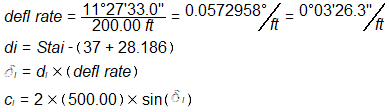
Curve table
| Station | di, ft | δi | ci, ft | ||||
| EC Back | 41+51.429 | 423.242 | = L | 24°15'00.0" | = Δ/2 | 410.719 | = LC |
| 41+00 | 371.814 | 21°18'12.1" | 363.306 | ||||
| 40+00 | 271.814 | 15°34'25.6" | 268.479 | ||||
| 39+00 | 171.814 | 9°50'39.1" | 170.970 | ||||
| 38+00 | 71.814 | 4°06'52.6" | 71.752 | ||||
| BC | 37+28.186 | 0.000 | 0°00'00" | 0.000 |
Deflection angles are all to the right.
Problem (2)
For the conditions below:
What are the deflection angle and radial chord at the BC to curve station 41+00.00?
Compute Δ
![]()
Determine BC station
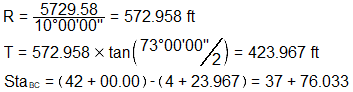
Set up and solve deflection equations for station 41+00
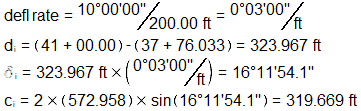
Answer: 319.67 ft at 16°11'54" Left.


