C. Error Theory
1. Error sources
Errors originate from one of three places:
- Natural - the conditions under which measurements are made.
- Instrumental - the equipment with which we make the measurements.
- Personal - the knowledge and skill of the people making the measurements.
We can control some of the errors within these sources, others we can’t. For example, while we can’t change the outside temperature we can compensate for it when measuring distances electronically.
2. Error types
While the source tells us where error comes from, it doesn’t tell us how it behaves; the error type does. There are technically three error types. “Technically” since some people don’t consider mistakes a type of error, but we’ll include it as it does affect measurements if present.
We'll briefly introduce error types and their effect on accuracy and precision in this chapter. Following chapters address each error in more detail and how they can be compensated or analyzed.
a. Mistake
A mistake is usually the result of carelessness or misunderstanding. Mistakes are generally isolated and stick out in a measurement set. They are common for people learning to use equipment for the first time - something gets forgotten, a wrong button is pushed, digits are transposed, etc.
b. Systematic
A systematic error is one which conforms to some mathematical or physical principle. This allows a systematic error to be compensated, provided we have enough information or measurements are repeated in particular fashion. Depending on the character of the error, compensation could be computational, procedural, or mechanical.
c. Random
Random errors are those left when mistakes are eliminated and systematic errors are compensated. They are the only errors which prevent our knowing the true value of what we’re measuring. Random errors tend to be small and as likely to be positive as negative. Repeating measurements multiple times give random errors a change to cancel.
3. Putting It Together
Anyway, let’s revisit our targets, Figure C-1, and see if we can make some observations on error sources and type.
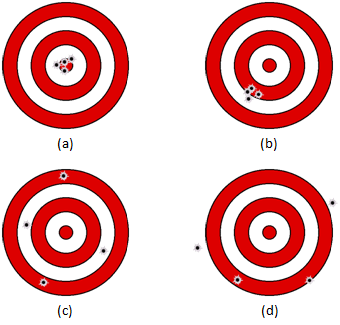 |
| Figure C-1 Accuracy and Precision |
- Target (a) shooter was both precise and accurate. This means the shooter has a pretty good handle on all the errors.
- Target (b) indicates the presence of a systematic error: shots are consistently low and left. To compensate, the shooter can either adjust the gun sights (mechanical) or aim high and right (procedural).
- Target (c) most likely results from a minimal experience shooter (error source: personal). On average the shooter has accurate results, but it’s achieved inefficiently. As the shooter gains experience, the efficiency increases and the pattern should begin to look more like (a).
- Target (d) can result from all sorts of error sources and types: inexperienced shooter (personal), windy conditions (natural), gun sights off (instrumental), throw in a possible mistake or two, and so on.
Because random errors are small and tend to cancel with repeated measurements we analyze them statistically. This is where we encounter terms like “standard deviation”, “95% confidence interval”, “least squares”, etc. We’ll look at basic analysis in Chapter F.
4. Equipment
In subsequent topics, equiipment use and measuring methods will be described. Included in each is a chapter on error source and behavior