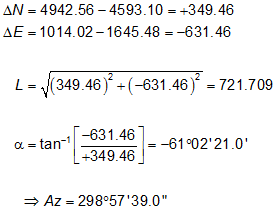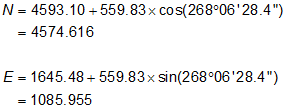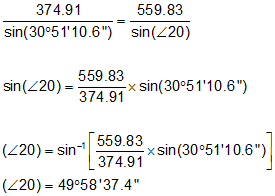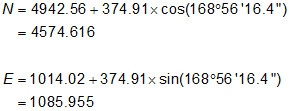E. Example Intersections
Two different intersection types are solved using triangle- and arc-based methods to demonstrate the different computation process. Additional decimal places will be carried in computations to minimize rounding errors.
1. Distance-distance
|
|
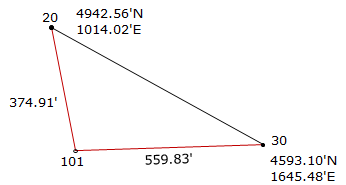
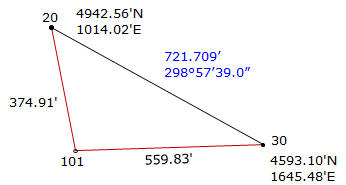
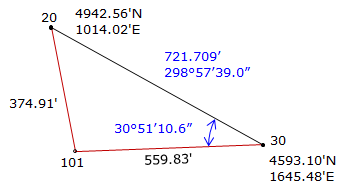
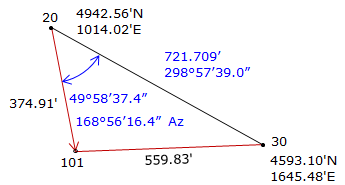
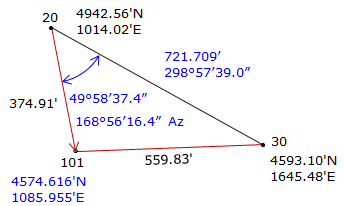
Given the information on the diagram, determine the coordinates of point 101.
|
|
Figure E-1 |
Step (1) For both methods is to inverse along the base line 30-20
|
|
 |
a. Triangle-based method
|
Step (2) Compute angle at 30 by Law of Cosines.
|
 |
|
Step (3) Compute direction from 30 to 101.
|
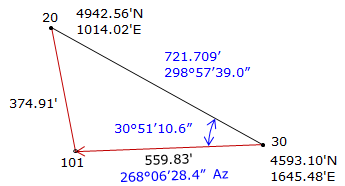 |
|
Step (4) Perform a forward computation from 30 to 101.
|
 |
Math Check: Compute coordinates from 20.
|
Step (1) Compute angle at 20 by Law of Sines.
|
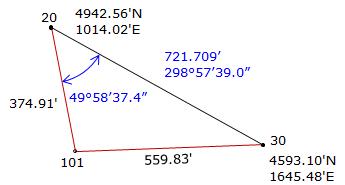 |
|
Step (2) Compute direction from 20 to 101.
|
 |
|
Step (3) Perform a forward computation from 20 to 101.
Both coordinates check. |
 |
b. Arc-based method
Step (2) Set up and solve Equations D-6 through D-9.
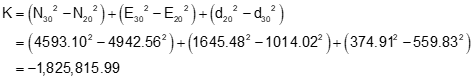
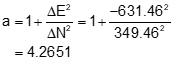
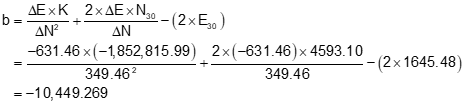
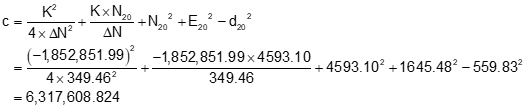
Step (3) Use Equations D-10 and D-11 to compute the two intersection points

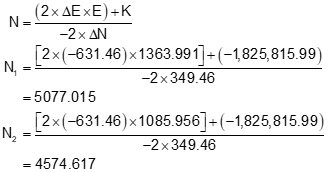
Step (4) Of the two, select the appropriate intersection point.
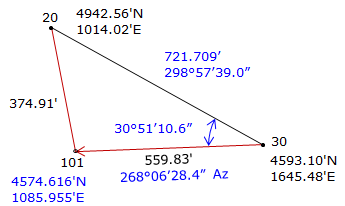
Point 101 is located southwest of the base line.
| Point | North | East | From base line |
| 1011 | 5077.015 | 1363.991 | north east |
| 1012 | 4574.617 | 1085.956 | south west |
The correct intersection point is 1012: (4754.617 ft N, 1085.956 ft E), same as the triangle-based solution.
2. Direction-distance
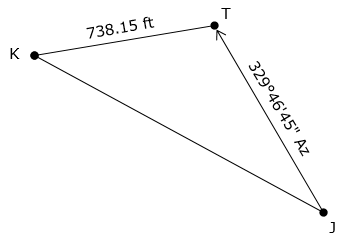
Figure xx-2 is a diagram of a base line and an intersection point.
|
|
|
Figure E-2 |
Coordinates of the base line end points are:
| Point | North (ft) | East (ft) |
| J | 1419.51 | 3511.69 |
| K | 2056.64 | 2341.36 |
The azimuth from point J to point T is 329°46'45"; the distance from point K to point T is 738.15 ft.
What are the coordinates of point T?
Step (1) Inverse the base line from point K to point J
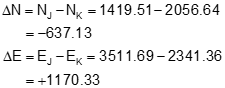
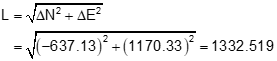

![]()
a. Triangle-based method
To get point T's coordinates, we'll perform a forward computation from K.
Step (2) Compute the angle at J
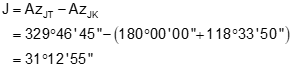
Step (3) Use Law of Sines to compute angle at T
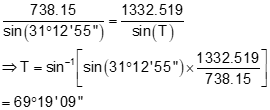
Remember that we have to check the angle returned by the Law of Sines because it will always be <90°.
From the diagram, T is greater than 90° so it must be subtracted from 180°
![]()
Step (4) Compute angle at K from the Angle Condition
![]()
Step (5) Compute azimuth from point K to point T
![]()
Step (6) Forward compute from point K
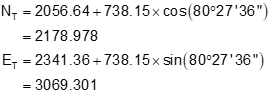
The math check is to compute the coordinates from point J
Step (1) Compute distance from point J using Law of Sines
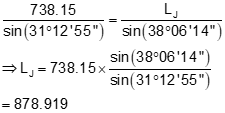
Step (2) Forward compute from point J

b. Arc-based method
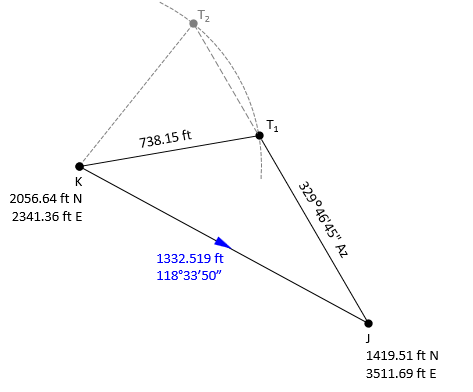
Because the direction can intersect the arc at two points, we'll extend the diagram a bit to visualize the possibilities, Figure XX-XX.
|
|
|
Figure E-3 |
Step (2) Set up and solve Equations D-12 through D-15.
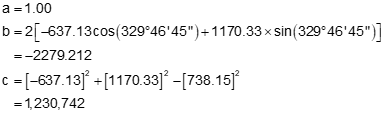
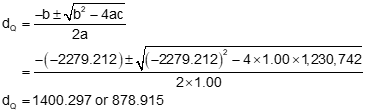
Step (3) Pick the correct distance and compute the coordinates
From Figure E-3, the correct distance dQ is the shorter one: 878.915,. Using that distance, perform a forward computation
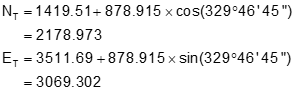
The coordinates of point T are the same as those from the triangle-based method.