F. More Intersection Types
1. Other types
Almost all other types of intersections are variations of distance-distance, direction-distance, and direction-direction.
a. Angle-distance
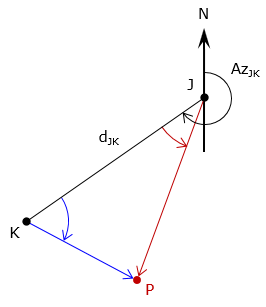
An angle-distance intersection, Figure F-1, is similar to direction-distance. The only difference is that angle-distance uses an angle and its turn direction from the base line. Otherwise, the solution process is the same.
|
|
|
Figure F-1 |
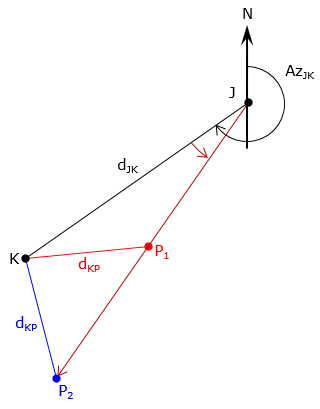
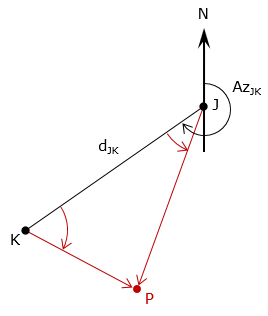
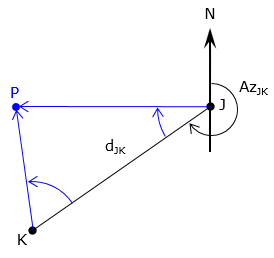
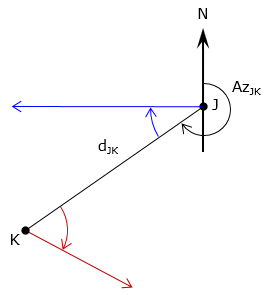
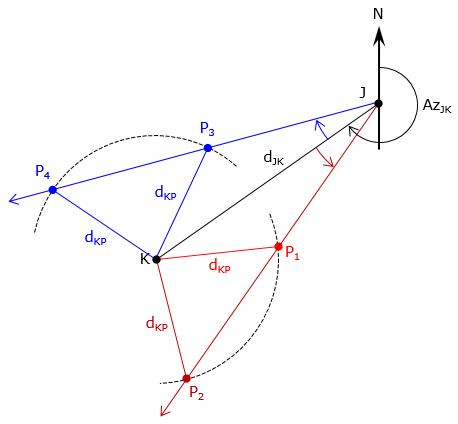
The angle turn direction (right/left, clockwise/counterclockwise) must be provided to prevent an ambiguity. Figure F-2 shows four different intersection points (two to the left, two to the right) depending on the direction of the angle at point J.
 |
|
Figure F-2 |
b. Angle-angle
An angle-angle intersection, Figure F-3, is similar to a direction-direction intersection. Instead of directions to the intersection point, angles at both ends of the base line are included. Directions can be computed from these angles. The solution process is the same as a direction-direction intersection.
|
|
|
Figure F-3 |
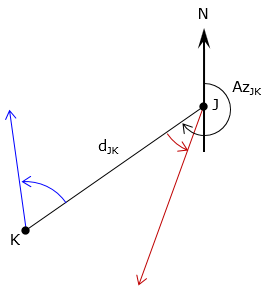
As with the angle-distance intersection, turn directions for each angle must be included. If turn directions are not included, there are four possible scenatoris, only two if which will result in an intersection, Figure F-4.
|
|
Angle J: (-) Angle K: (+)
|
|
|
Angle J: (+) Angle K: (-) |
|
|
Angle J: (+) Angle K: (+) No intersection |
|
|
Angle J: (-) Angle K: (-) No intersection |
|
Figure F-4 |
|
c. Arc-arc
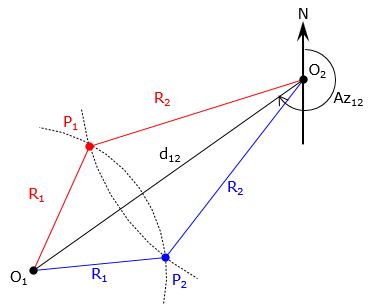
An arc-arc (circle-circle) intersection, Figure F-5, is the same as is a distance-distance intersection. The radius point of each arc defines the base line and their respective radii are the two distances. As with a distance-distance intersection, there are two possible points and they would be solved for the same way.
|
|
|
Figure F-5 |
d. Direction-arc
Figure F-6, is an direction-arc (direction-circle) intersection which is the same as a direction-distance intersection. A line at a specific direction starts at one end of the base line and intesects an arc centered on the other end.
|
|
|
Figure F-6 |
As in the angle-distance intersection, the angle turn direction must be defined otherwise we have the same situation as shown in Figure F-2. The solution process is the otherwise same as the distance-direction method.
e. Angle-arc
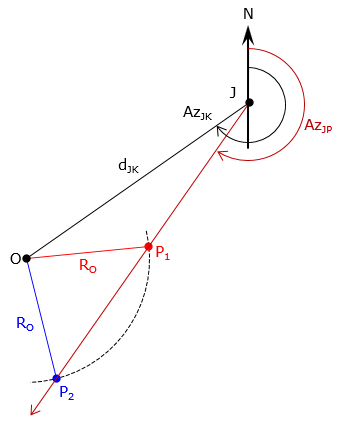
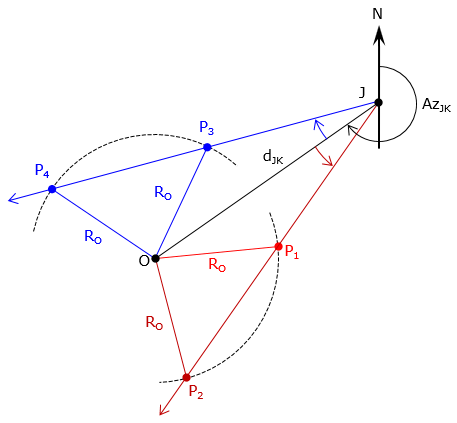
A line at a specific angle at one end of the base line intersects an arc centered on the other end of the base line. This is the same as the angle-distance intersection and like that type, the angle turn direction must be specified otherwise the ambiguous situation in Figure F-7 will result.
 |
|
Figure F-7 |
2. Field Variations
In all the methods discussed direction and/or distance measurements were made from both ends of the base line. In order to turn an angle from one end of the base line, the other end must be visible to serve as a back sight. In the field, this isn't always practical or efficient. The key to intersection solution is that the unknown point must be visible from both ends of the base line, or, conversely, the end points are visible from the unknown point. This allows the surveyor to make a single instrument set up - at the unknown point.
a. Determining instrument location
|
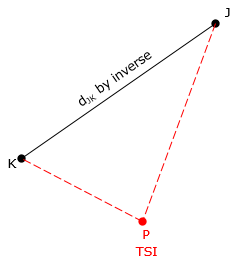
The base line still forms a known side of the triangle even if the end points are not inter-visible. That means two other measurements are necessary in order to fix the triangle. With a total station instrument (TSI) set up at the unknown point, Figure F-8, what measurements should be made? |
|
|
Figure F-8 |
|
|
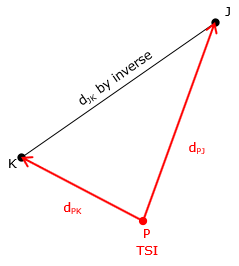
Distance-distance, Figure F-9
|
|
|
|
|
|
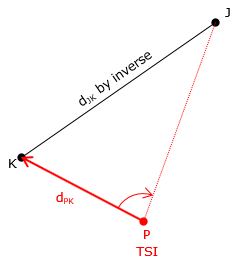
Distance-angle, Figure F-10
|
|
|
|
|
|
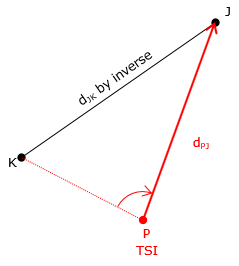
Angle-distance, Figure F-11
|
|
|
|
|
|
Distance-angle-distance, Figure F-12
|
b. Determining length of obstructed line
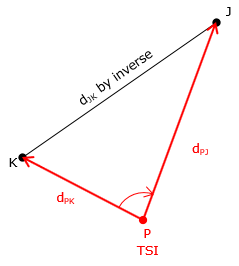
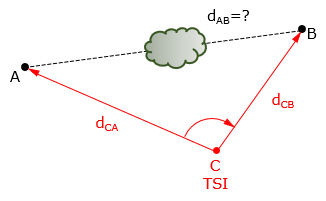
Sometimes it's not the TSI location that is desired, but the distance between two non-inter-visible points. For example, the sight between two adjacent property corners may be blocked due to intermediate obstacles such as trees. The surveyor, however, can find a TSI location from which both points can be seen. The distances to and angle between the points can be measured from the TSI, Figure F-13.
|
|
|
Figure F-13 |
This is called the missing line method since the desired line cannot be directly measured. Two distances and one angle measured are three elements of the triangle. The missing distance can be calculated using the Law of Cosines.
c. Leave it to the instrument
Being instrument-centric procedures, most TSI have onboard computational routines for instrument location and missing line determination providing sufficient measurements are made.