a. Traverse with Bearings
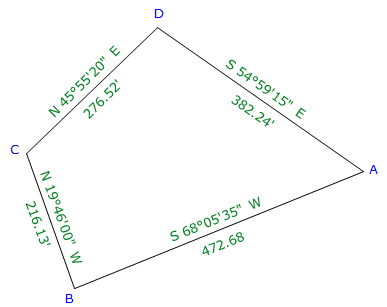 |
| Figure E-6 Bearing Traverse Example |
| Line | Bearing | Length (ft) | Lat (ft) | Dep (ft) |
| AB | S 68°05'35"W | 472.68 | -176.357 | -438.548 |
| BC | N 19°46'00"W | 216.13 | +203.395 | -73.093 |
| CD | N 45°55'20"E | 276.52 | +192.357 | +198.651 |
| DA | S 54°59'15"E | 382.24 | -219.312 | +313.065 |
| sums: | 1347.57 | +0.083 | +0.075 | |
| Distance | Lat err too far N |
Dep err too far E |
(1) Adjust the Lats and Deps
Setup Equations E-1 and E-2:
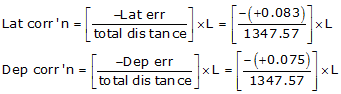
Now solve Equations E-3 and E-4 for each line:
Line AB
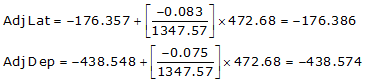
Line BC
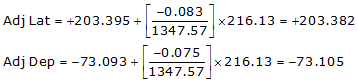
Line CD
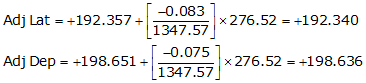
Line DA
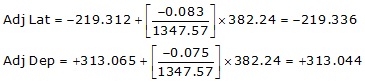
Check the closure condition
| Adjusted | ||
| Line | Lat (ft) | Dep (ft) |
| AB | -176.386 | -438.574 |
| BC | +203.382 | -73.105 |
| CD | +192.340 | +198.635 |
| DE | -219.336 | +313.044 |
| sums: | 0.000 | 0.000 |
| check | check | |
A common mistake is to forget to negate Lat err and Dep err in the correction equations. If that happens, the closure condition will be twice what it originally was as the corrections were applied in the wrong direction.
(2) Compute adjusted lengths and directions
Use Equations E-5 and E-6 along with Figure E-5 to compute the new length and direction for each line.
Line AB
Adj Lat = -176.386 <- South
Adj Dep = -438.574 <- West
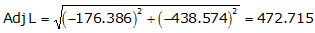
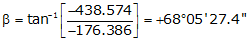
Because it's the SW quadrant, Brng =S 68°05'27.4" W.
Line BC
Adj Lat = +203.382 <- North
Adj Dep = -73.105 <- West
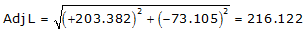
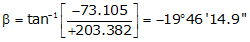
Because it's the NW quadrant, Brng = N 19°46'14.9" W
Line CD
Adj Lat = +192.340 <- North
Adj Dep = +198.635 <- East
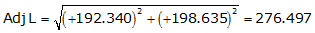
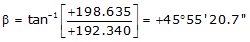
Because it's the NE quadrant, Brng = N 45°55'20.7" E
Line DA
Adj Lat = -219.336 <- South
Adj Dep = +313.044 <- East
![]()
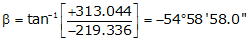
Because it's the SE quadrant, Brng = S 54°58'58.0" E
(3) Adjustment summary
| Adjusted | Adjusted | |||
| Line | Lat (ft) | Dep (ft) | Length | Bearing |
| AB | -176.386 | -438.574 | 472.715 | S 68°05'27.4" W |
| BC | +203.382 | -73.105 | 216.122 | N 19°46'14.9" W |
| CD | +192.340 | +198.635 | 276.479 | N 45°55'20.7" E |
| DE | -219.336 | +313.044 | 382.237 | S 54°58'58.0" E |