F. Coordinates
1. General
Point position can be expressed in relative or absolute terms.
a. Relative position
A relative position is the either the (a) length and direction, or, (b) latitude and departure between two points.
Give the adjusted traverse of Figure F-1:
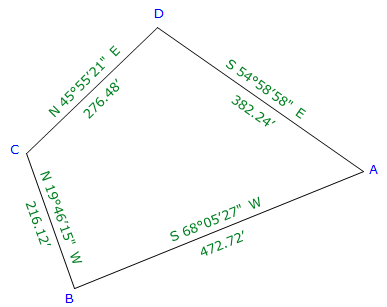 |
| Figure F-1 Adjusted Loop Traverse |
Lengths and directions around a traverse define the relative locations of successive traverse points.
Point B is 472.72 feet from point A at a bearing of S 68°05'27"W.
Point C is 216.12 feet from point B at a bearing of N 19°46'15"W.
In terms of latitudes and departures:
Point B is 176.39 feet South and 438.57 feet West of point A.
Point C is 203.38 feet North and 73.10 feet West of point B.
Where is point C relative to point A? Because the two points are not directly connected on the traverse, it requires a little more computing.
Lat A to C: [-472.72 ft x cos(68°05'27") + 216.12 ft x cos(19°46'15")] = +26.99 ft
Dep A to C: [-472.72 ft x sin(68°05'27") - 216.12 ft x sin(19°46'15")] = -511.68 ft
Point C is 28.99 ft North and 511.68 ft West of point A. We could compute the lats and deps through point D instead of point B - the distances from point A to point C would be the same.
b. Absolute Position
An absolute position is a distance from a datum. In the case of a traverse point, two horizontal lines serve as the data. One line corresponds with the meridian, the other is perpendicular to it, Figure F-2.
 |
| Figure F-2 Horizontal Datum |
The meridional line is called either the Y or North (N) axis; the other the X or East (E) axis.
A point position is expressed as a coordinate pair are represent perpendicular distances from the two axes.
For example:
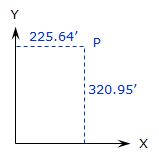 |
In terms of an X and Y system, Figure F-3, the coordinates of point P are X=225.64' and Y=320.95' |
| Figure F-3 X and Y System |
|
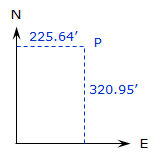 |
In terms of an North and East system, Figure F-4, the coordinates of point P are E=225.64' and N=320.95' |
| Figure F-4 North and East System |
2. Coordinates Computations
a. Forward Computation
A forward computation uses a starting coordinate pair along with a distance and direction to determine another coordinate pair.
In Figure F-5, starting with coordinates at P, compute the coordinates at Q.
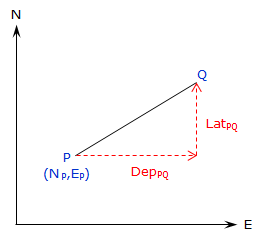 |
| Figure F-5 Forward Computation |
Using Equations D-1 and D-2, the latitude and departure of the line are:
|
LatPQ= LPQx cos(DirPQ) DepPQ = LPQ x sin(DirPQ) |
|
L: line length |
To compute X and Y coordinates:
|
YQ = YP + LatPQ XQ = XP + DepPQ |
Equations F-1 and F-2 |
To compute N and E coordinates:
|
NQ = NP + LatPQ EQ = EP + DepPQ |
Equations F-3 and F-4 |
For a complete traverse, Figure F-6:
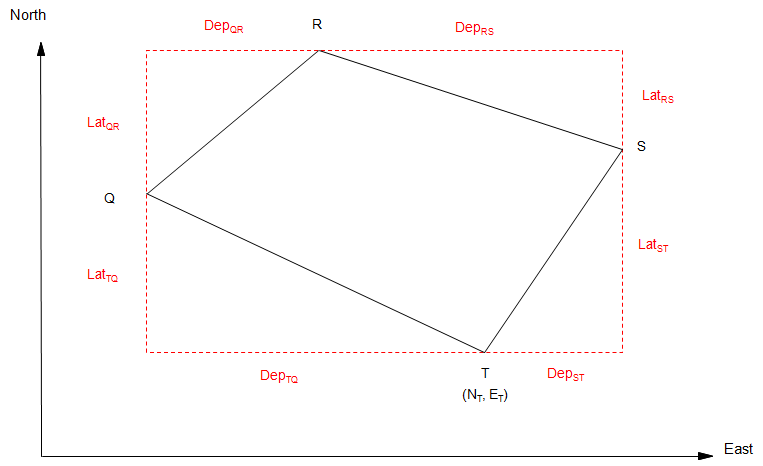 |
| Figure F-6 Coordinates Around a Loop Traverse |
Starting with known coordinates at T (NT, ET) and applying Equations F-3 and F-4 around the traverse:
| Compute coordinates of Q: | 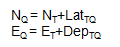 |
| Compute coordinates of R: | 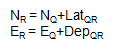 |
| Compute coordinates of S: | 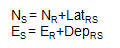 |
| Compute coordinates of T: | 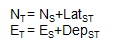 |
Computing back into T gives a math check: the end coordinates should be the same as the start coordinates.
In order for the math check to be met, adjusted lats and deps must be used.
Where do the start coordinates come from? They can be assumed or they could be from a formal coordinate system. We'll discuss formal coordinate systems in a later topic.
b. Inverse Computation
An inverse computation is used to determine the distance and direction between two coordinate pairs. The computations involved are basically the same as those for determining a line's new length and direction from its adjusted lats and deps.
For the traverse shown in Figure F-7, how would we determine the length and direction of the line from point T to point R?
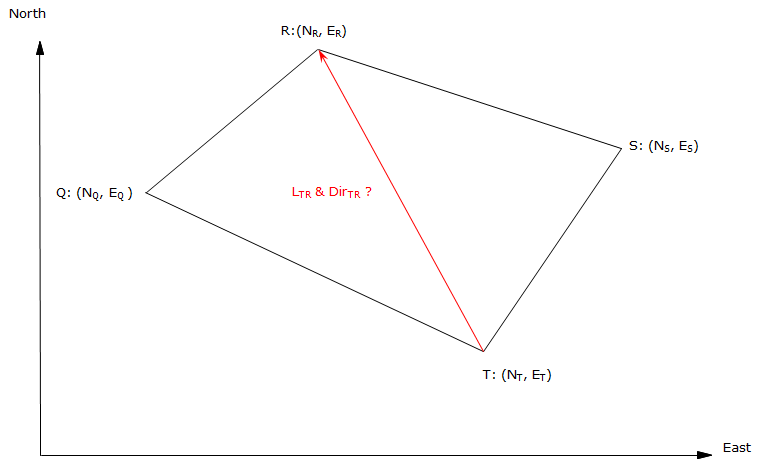 |
| Figure F-7 Length and Direction Between Nonadjacent Points |
Knowing the coordinates of the two points, we can determine the latitude and departure of the line from the coordinate differences, Figure F-8.
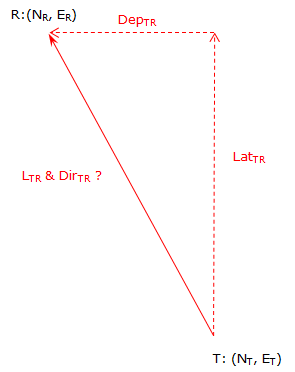 |
|
Figure F-8 |
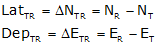 |
Equations F-5 and F-6 |
Note that the differences are the To point values minus the From point values.
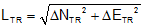 |
Equation F-7 | |
| and | ||
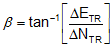 |
Equation F-8 | |
| where | ||
| -90° ≤ ß ≤ 90° |
The mathematic signs on the coordinate differences determine the direction quadrant, Figure F-9.
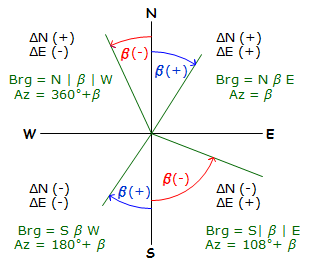 |
| Figure F-9 Converting ß to a Direction |
If X and Y coordinates are used, remember that Y corresponds to N and X corresponds to E.
3. Examples
a. Traverse 1
(1) Forward Computation
 |
|
Figure F-10 |
| Adjusted | ||
| Line | Lat (ft) | Dep (ft) |
| AB | -176.386 | -438.574 |
| BC | +203.382 | -73.105 |
| CD | +192.340 | +198.635 |
| DE | -219.336 | +313.044 |
The coordinates of point A are 500.000' N, 2000.000' E. Compute the coordinates of the remaining points.
A simple way is to set up a table with North coordinates and latitudes in one column, East coordinates and departures in another.
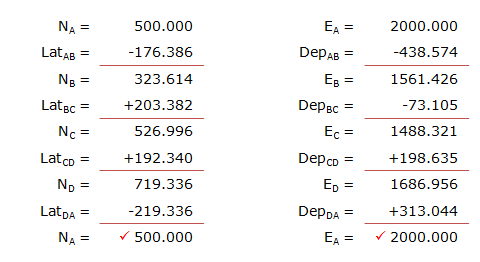
(2) Inverse Computation
What are the length ad bearing of the line A to C in the diagram below?
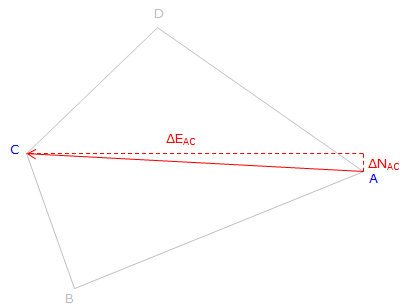 |
| Figure F-11 Length anf Direction Determination |
From Equations F-5 and F-6:
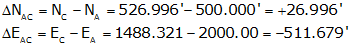
Substituting into Equation F-7
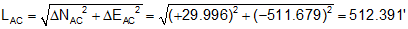
and Equation F-8
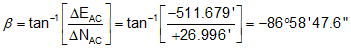
Because ΔN is North and ΔE is West: N86°58'47.6"W
Line AC: 512.39' at N86°58'48"W
b. Traverse 2
(1) Forward Computation
The crossing traverse in Figure F-12 was previously adjusted with the results shown below.
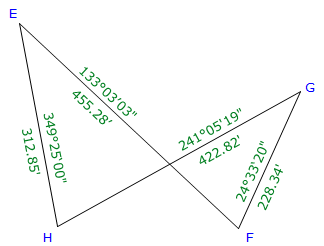 |
| Figure F-12 Crossing Traverse Forward Computation |
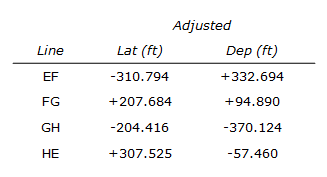
The coordinates of point E are 200.000' X, 1000.000' Y.
Compute the coordinates of the remaining points.
Arranging the computations in a table:
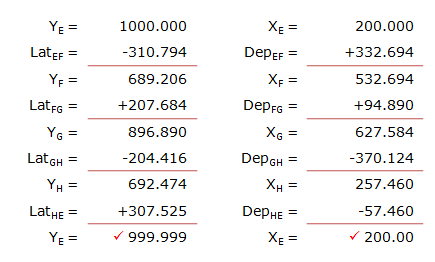
(2) Inverse Computation
Determine the length and azimuth of the line from point F to point H.
Remember: Y=>N, X=>E; and it's To minus From.
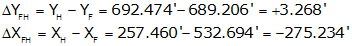
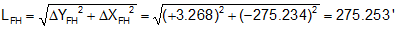
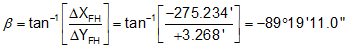
Because ΔY is North and ΔX is West:
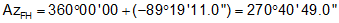
Line FH: 275.25' and azimuth of 270°40'49".
4. Closing
Although including coordinates involves addition computations, they provide ability to indirectly determine other values. We saw examples here where the distance and direction can be determined between points not directly connected on a traverse. This is very useful where lines may be obstructed but we still need their length and direction. We will see in the next section how coordinates facilitate area computation.
Later still in the Coordinate Geometry topic, we'll see how integrating forward and inverse computations with trigonometric principles allow for greater field measurement and computational flexibility.