5. Thin Lens
a. Description
A thin lens is a narrow medium that has at least one curved surface for gathering light rays from distant objects. One or both sides of the lens are spherically convex or concave surfaces. Curvature radii and material density affect the lens' refraction and focusing characteristics. Figure H-10 shows just a few possible lens types.
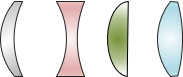 |
| Figure H-10 Different Thin Lenses |
To the human eye, a distant object may be hard to see while a close one too small to make out detail. Visible objects emit light rays in all directions. A lens collects these rays to create an image that is generally larger than perceived with the naked eye, Figure H-11.
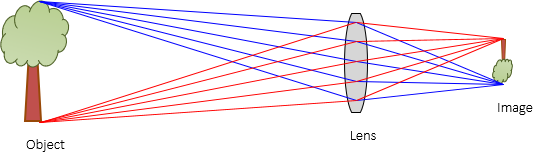 |
| Figure H-11 Lens Use |
b. Focal length
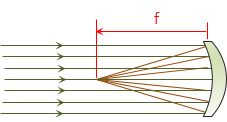
The curved surface(s) together with Snell's Law cause the light rays to converge on one side of the lens. Light rays from an object at infinity (or at least very far away) are parallel and converge to a point at a specific distance from the lens. That distance is the focal length, f, of the lens, Figure H-12.
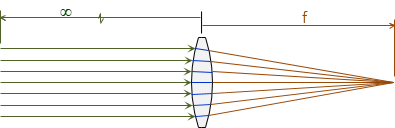 |
| Figure H-12 Parallel Rays and Focal Length |
Even if oblique to the lens, Figure H-13, parallel light rays converge at the focal distance, although the focus point shifts parallel with the lens.
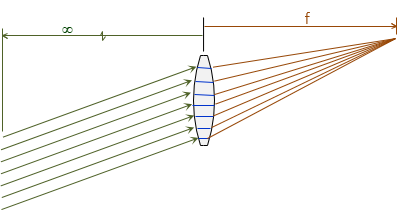 |
| Figure H-13 Oblique Light Rays |
The focal length is computed using Equation H-4.
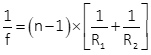 |
Equation H-4 |
|
n: refractive index of lens material |
|
Using the convention of light rays traveling from left to right as in Figure H-11, R1 is radius of the left lens surface facing the object, R2 is the right surface.
- R1 is positive if its curvature center is on the image side, negative on the object side.
- R2 is positive if its curvature center is on the object side, negative on the image side.
The radius of a flat side is infinity.
Figure H-14 shows radius sign conventions for a few different lens types.
 |
| Figure H-14 Radii Sign Convention |
If the focal length is positive, the lens is a convergent lens, a negative focal length makes it a divergent lens. The image formed by a convergent lens is on the side opposite that of the object's, Figure H-15; the image of a divergent lens is on the same side as the object, Figure H-15.
 |
| Figure H-15 Divergent Lens |
Example:
What is the focal length of the lens shown below? Its refractive index is 1.54.

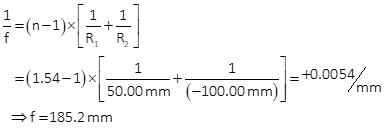
c. Optical axis
The optical axis is a line connecting the curvature centers of both sides, Figure H-16(a). For a lens with one flat side, it is the line from the curvature center perpendicular to the flat side, Figure H-16(b).
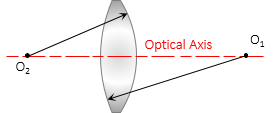 (a) Two curved surfaces |
 (b) One flat surface |
| Figure H-16 Optical Axis Definition |
d. Focal point; Focal plane
The focal point located on the optical axis at the focal distance. The focal plane is perpendicular to the optical axis at the focal point. Figure H-17.
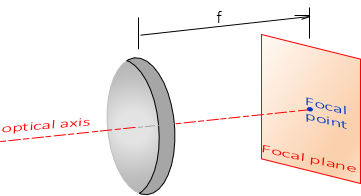 |
| Figure H-17 Focal Point and Plane |
Light rays parallel with or oblique to the optical axis will come to focus at a point somewhere the focal plane.
e. Lens Equation; Image plane
The focal length is the distance at which an object located at infinity will come to focus. When the object distance is much less than infinity, the lens must be moved relative to the focal plane for the image to be sharp. The Lens Equation, Equation H-5, defines object and image distances and focal length relationships.
| Equation H-5 | |
|
f: focal length |
|
For a given lens, its focal distance is fixed; changing the object distance changes the image distance. As object distance approaches infinity, image distance approaches the focal length., Figure H-18.
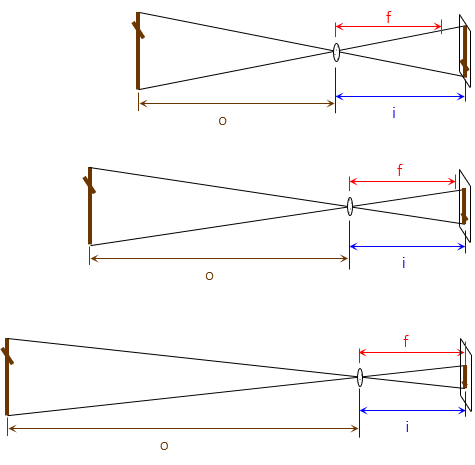 |
| Figure H-18 Object and Image Distance Behavior |
Consider a Single Lens Reflex (SLR) camera, Figure H-19: to focus on an object, the lens barrel is rotated which moves the lens in and out changing the image distance. This is a mechanical solution of the lens equation.
 |
| Figure H-19 Focusing a 35mm Camera |
The image plane is similar to the focal plane except it moves as the image distance changes. The image and focal planes coincide for distance objects.
Example
A camera has a 135 mm focal length lens. Determine image distances for 1, 10, 100, and 1000 meter object distances.
Re-arrange Equation H-5 to solve it in terms of image distance. Because object distances are in meters, include a meter to millimeter conversion factor:
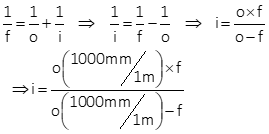
At 1 m object distance:
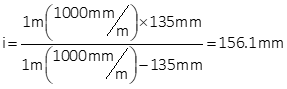
Substituting the remaining object distances:
| Object dist, m | Image dist, mm |
| 1 | 156.1 |
| 10 | 136.8 |
| 100 | 135.2 |
| 1000 | 135.0 |
Notice how the image distances approach the focal length as shown in Figure H-18.
e. Flip it
A single thin lens inverts the image which isn't an issue for many applications. For others, like the view through an instrument's telescope, an upright image is preferred. Adding a second lens will re-invert the image, Figure H-20.
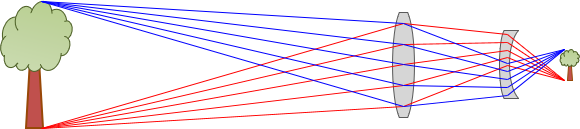 |
| Figure H-20 Upright Image |