2. Network Adjustment Methods
Network adjustment is the method by which the misclosure is distributed back into the newly created elevations. The adjustment methodology should reflect error behavior and be repeatable. There are a number of approaches, some better than others. These are summarized in Table E-2.
| Table E-2 | |||
| Method | Premise | Advantage | Disadvantage |
| Ignore | Don't adjust anything. | Simple; repeatable. | Ignores errors. |
| Arbitrary | Place error randomly in one or more raw elevations. | Simple. | Not repeatable. |
| Judgement call | Decide based on field conditions, equipment, and personnel, which raw elevations probably had more error. | Considers error behavior. | Not repeatable; not rigorous; requires personal knowledge of entire project. |
| Equal distribution | Distribute errors equally among raw elevations. | Simple; repeatable. | Treats random errors systematically; assumes all errors are positive or negative. |
| Proportional distribution | Distribute errors based on sight distances. | Simple; repeatable; accounts for greater error in longer sights. | Treats random errors systematically; assumes all errors are positive or negative; requires distances. |
| Least squares | Full statistical approach. | Allows full random error modeling; can mix different quality measurements; provides adjusted elevation uncertainties. | Most complicated and computation-intensive. |
For simple networks, Figure E-2(a), the Equal or Proportional distributions generally give satisfactory results. However in complex networks which have additional measurements between points, Figure E-2(b), using the Equal or Proportional methods is too cumbersome if not impossible.
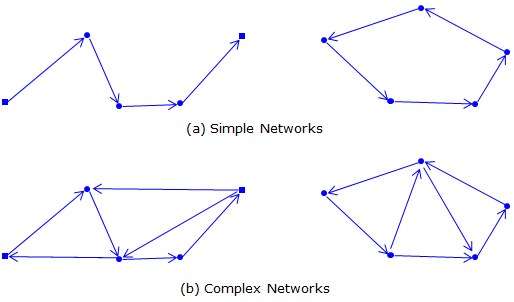 |
| Figure E-2 |
In a simple network, each point has only a single raw elevation. In a complex network, each point can have multiple raw elevations based on connections to other points. The raw elevations differ because their respective random errors accumulated along different paths to the point. The best way to model and compensate the errors is using least squares.
The concept of least squares is beyond the scope of this discussion since we are limiting it to simple networks. We will look at applying the Equal and Proportional methods.