Article Index

Page 2 of 4

2. Arcs

Geometric curved lines are generally sections of circular arcs since those are the most prevalent in horizontal alignments.

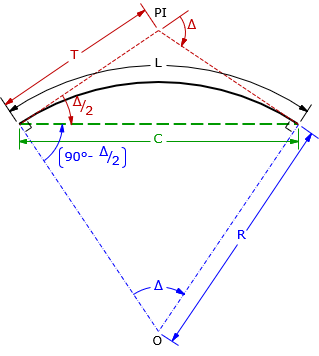
a. Geometric elements; Nomenclature
  • PI: Point of Intersection; where the tangent lines intersect
  • Δ: central angle; also the deflection angle between tangents
  • R: radius
  • L: arc length
  • C: chord length
  • T: tangent distance; both tangents are the same length
  • The angle between the tangent and chord is half the central angle: Δ/2
  • The angle between the chord and radial line at each curve end is (90°-Δ/2)

Figure G-2
Arc parts and nomenclature

The primary geometric elements are related through Equations G-1, G-2, and G-3.

Equation G-1

Equation G-2

Equation G-3

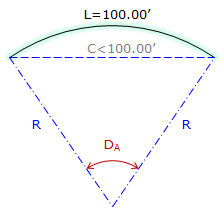
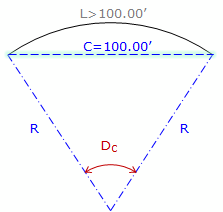
When dealing with highway or railroad alignments, an additional geometric element is often specified: degree of curvature, D. There are two different degree of curvature definitions:

  • DA, arc definition; the angle subtended by a 100.00' arc, Figure G-3(a)
  • DC, chord definition; the angle subtended by a 100.00' chord, Figure G-3(b)

(a) Arc definition

(b) Chord definition

Figure G-3
Degree of curvature

Arc definition is used in highway and street design while the Chord definition is used in railroad design. Because each definition differs, there is a slightly different radius relationship for each:

Equation G-4

Equation G-5

R in feet, D in deg-min-sec

Degree of curvature is an exclusively English units system attribute as there is no 100.00' equivalent in the metric system. Because of this, we won't use it here in the COGO section.

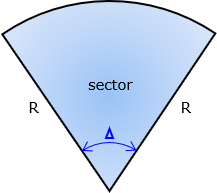
b. Sectors; Segments

Sectors and segments are parts of a circle and are used to compute areas enclosed by curvilinear boundaries.

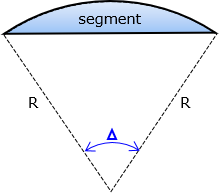
  • A sector is a wedge of a circle bound by the arc and radial lines spaced Δ apart, Figure G-4.
  • A  segment is the area between the arc and its chord, Figure G-5.

Figure G-4
Sector
 

Figure G-5
Segment
 

Equation G-6

Equation G-7
Details
Hits: 13555