4. Traverse with curves
a. Arc incorporation
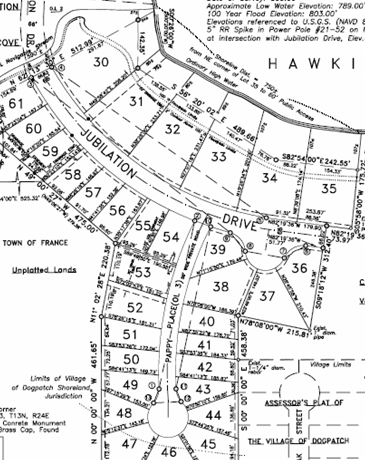
To incorporate a curve in a traverse requires defining the curve's geometry and its tangency conditions at both ends. To fix an arc's geometry, at least two of its geometric elements (e.g., R, Δ, L, T, C) must be fixed. COGO tools can be used with arc geometry and orientation to compute point positions. This gives us the ability to compute more complex collections of traverses such as Figure G-9 (taken from the Example Plats section of the Wisconsin Platting Manual, Plat Review, Wisconsin Dept of Administration).
|
|
|
Figure G-9 |
b. Simple curvilinear traverse example
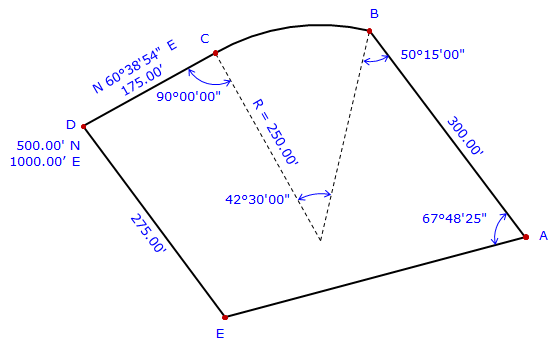
Given the traverse data in Figure G-10.
|
|
|
Figure G-10 |
Curve BC is non-tangent at point B, tangent at point C.
Explain how to determine to coordinates of the traverse points.
|
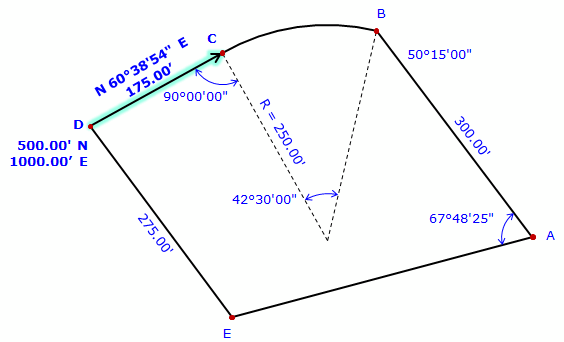
We have to start where there are coordinates. In this case, that's at point D. From point D we can go to either point E or point C. There isn't enough information to compute point E's coordinate, but there is to compute point C's. Perform a Forward Computation to point C. |
|
|
|
 |
|
From point C we can compute point B's coordinates two ways:
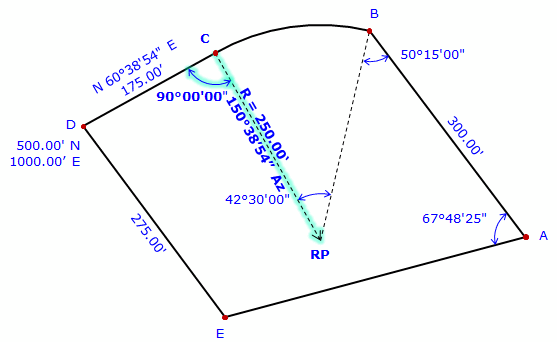
We'll use the first way: Compute direction from point C to radius point: Az = (60°38’54”+180°)-90°00’00” = 150°38’54” Perform a Forward Computation to radius point, RP. |
|
|
|
 |
|
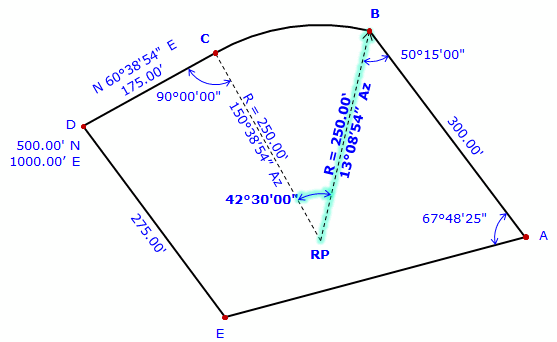
At the radius point, compute direction to point B. Az = (150°38'54"+180°00'00") + 42°30'00" = 373°08'54" = 13°08'54" Perform a forward computation to point B. |
|
|
|
 |
|
At point B, compute direction to point A. Az = (13°08'54"+180°00'00) - 50°15'00" = 142°53'54" Perform a Forward Computation to point A. |
|
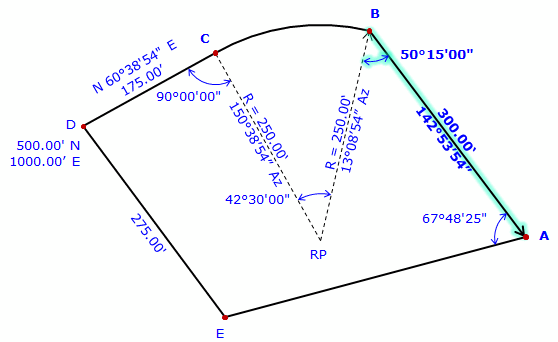 |
|
|
There isn't sufficient data to perform a Forward Computation from point A to point E. Point E is also connected to point D but there isn't enough data to perform a Forward Computation from point D. However, point E can be determined by a Direction-distance intersection using its connections to points A and D. Compute direction from point A to E Az = (142°53'54"+180°00'00") - 67°48'25" = 255°05'29" Compute the Direction-distance intersection |
|
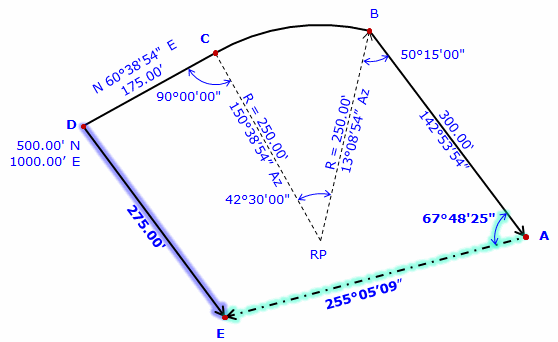 |
|