3. Azimuth from Interior Angles
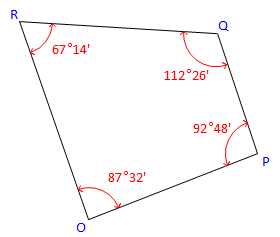
Given the following traverse and horizontal angles:
|
|
|
Figure C-28 |
Using a azimuth of 68°00' for line OP, determine the azimuths of the remaining lines counter-clockwise around the traverse.
|
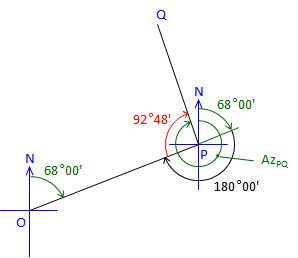
At point P: |
|
|
Figure C-29 |
Line PQ is 92°48' right of Azimuth PO Az PO is the back azimuth of Az OP Az PQ = (Az OP + 180°00') + Angle PAz PQ = (68°00' + 180°00') + 92°48' = 340°48' |
|
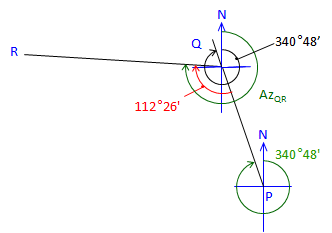
At point Q: |
|
|
Figure C-30 |
Line QR is 112°26' to the right from Az QP Az QP is the back azimuth of Az PQ Az QR = (Az PQ + 180°00') + Angle QAz QR = (340°48'+180°00') + 112°26' = 633°14' Normalize: Az QR = 633°14' - 360°00' = 273°14' |
|
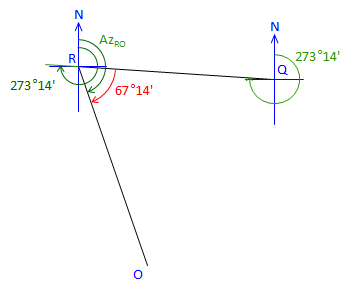
At point R: |
|
|
Figure C-31 |
Line RO is 67°14' right from Az RQ Az RQ is the back azimuth of Az QR Az RO = (Az QR + 180°00') + Angle RAz RO = (273°14' + 180°00') + 67°14' = 520°28' Normalize: Az RO = 520°28' - 360°00' = 160°28' |
|
The directions for all four traverse lines have been computed. Angles at P, R, and R have been used, but not the angle at O. For a math check, use Azimuth RO and the angle at O to compute the original Az OP. |
|
|
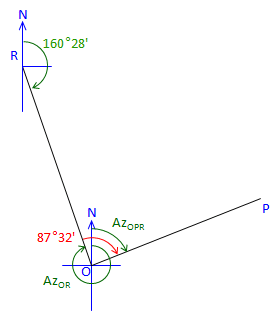
At point O: |
|
|
Figure C-32 |
Line OP is 87°32' right of Az OR Az OR is the back azimuth of Az RO Az OP = (Az RO + 180°00') + Angle O Az OP = (160°28' + 180°00') + 87°32' = 428°00' Normalize: Az OP = 428°00' - 360°00' = 68°00' check! |
Summary:
| Line | Bearing |
| OP | 68°00' |
| PQ | 340°48' |
| QR | 273°14' |
| RO | 160°28' |
There's a distinct pattern computing these azimuths:
New Az = (Previous Az + 180°00') + Angle.
This is true for a loop traverse meeting these conditions:
- Directions are counter-clockwise around the traverse, and,
- Angles are interior to the right.
What if the directions are clockwise around the traverse and interior angles counter-clockwise?
New Az = (Previous Az - 180°00') - Angle
Other patterns exist for clockwise travel with clockwise interior angles, clockwise exterior angles, counterclockwise exterior angles, etc. Rather than memorize the possible patterns, draw a sketch, and begin computing; the pattern will present itself after a few lines.