5. Azimuths from Deflection Angles
Deflection angles are measured traveling clockwise around a loop traverse. Starting with an azimuth of 328°58'15" for line AB, determine azimuths of the remaining lines.
(a) Check angular misclosure.
Since this is a non-crossing loop traverse, the deflection angle sum should be ±360°00'00". Right deflection angles are positive, left are negative.
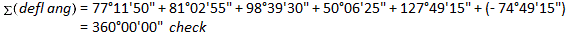
There is no misclosure to distribute.
(b) Compute azimuths
Starting with the azimuth of line AB
Line AB's extension through B has the same azimuth as line AB.
Because the deflection angle to line BC is measured from the extension of line AB, the azimuth of line BC is the azimuth of line AB plus the deflection angle:
Since the azimuth exceeded 360°, it is normalized by subtracting 360° from it.
Continuing to line CD, we use the same logic: New azimuth = previous azimuth + deflection angle
And so on...
At point D
Finally, at point A compute back into the first azimuth to make sure there are no math errors:
