C. Subtense Bar

1. Principle

a. Tacheometry

Tacheometry is distance determination by passive optical methods. It uses an optical instrument at one end and an observable scale or known length at the other. It is passive because it is based on visual observation and geometry measurement and does not use artificial energy.

b. Using a subtense bar

A subtense bar is one tacheometric method and the subject of this chapter. It is a physical bar with sighting targets at both ends. The distance, d,  between the targets is known, Figure C-1.

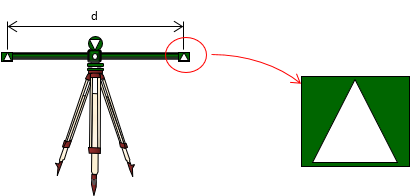Figure C-1 Subtense Bar

The bar is set up on a tripod at one end of a line, centered on and perpendicular to it. At the other end is a transit or theodolite, Figure C-2.

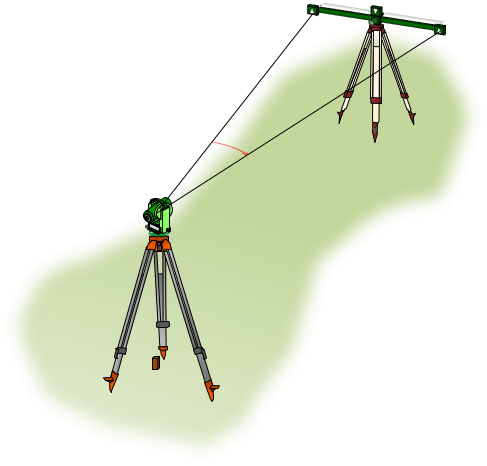Figure C-2 Set up

The horizontal angle between the two targets is measured with the transit/theodolite, Figure C-3.

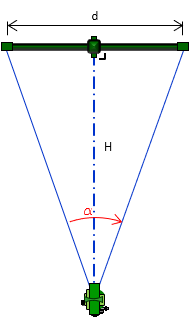Figure C-3 Measure Horizontal Angle

The horizontal distance, HD, is obtained by using Equation C-1.

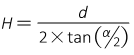Equation C-1