3. Example Computations
a. Measurement Set
Let's compute the statistics of our measurement set: 45.66 45.66 45.68 45.65
(Keep in mind that this is an absurdly small measurement set hardly worthy of statistical analysis. We're using it only to demonstrate the random error analysis process).
| Step (1) | Step (2) | Step (3) | |
| num | value | v = meas-MPV | v2 |
| 1 | 45.66 | 45.66-45.662 = -0.002 | 0.000004 |
| 2 | 45.66 | 45.66-45.662 = -0.002 | 0.000004 |
| 3 | 45.68 | 45.68-45.662 = +0.018 | 0.000324 |
| 4 | 46.65 | 45.65-45.662 = -0.012 | 0.000144 |
| sums | 182.65 | 0.000476 |
(1) Compute MPV, Equation F-1
According to the rules of significant figures, the measurement sum has 5 sig fig.
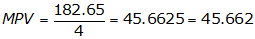
In addition to isolating errors, repeating measurements can also increase accuracy. In this case, we’ve gone from 0.01 units to 0.001 units. Of course, the more measurements made, the stronger that additional accuracy. Four measurements, as in our example, are not really enough for a true statistical picture.
(2) Compute the residuals
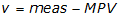
Since this represents an intermediate computation, carry an additional digit. Residuals have the same units as the measurements.
(3) Square and sum the residuals
Keeping in mind the addition rule for significant figures, the measurement sum has 3 sig fig.
By the way, the term least squares comes from the fact the MPV is the number which results in the smallest (or least) sum of the squares of the residuals. Any other number will result in a larger sum.
(4) Compute the standard deviation, Equation F-2
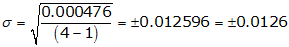
The standard deviation has the same units as the measurements.
(5) Compute the Error of the MPV, Equation F-4
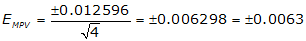
The error of the MPV has the same units as the measurements.
(6) Results
From (1), the MPV is good to 0.001
We should express the standard deviation and error of the mean to the same resolution level.
MPV = 45.662 ±0.013; EMPV = ±0.006
So what’s all this mean? Based on our measurements:
- The most probable value of the measured quantity is 45.662;
- 68% of our measurements fall within ±0.013 of the MPV;
- The error in the MPV is expected to be ±0.006.
b. Example with Angles
One of the problems working with angles is the tendency to carry insufficient digits when converting from deg-min-sec to decimal degrees. For some reason, three decimal places seems to be the norm but this can cause substantial rounding error computing measurement statistics.
To demonstrate this, lets look at a simple example consisting of 4 angles: 168°42'30", 168°42'10", 168°42'15", and 168°42'25".
(1) Convert to and carry three decimal places.
| Angle | Decimal Deg | v; deg | v2; deg2 |
| 168°42'30" | 168.708 | +0.002 | 0.000004 |
| 168°42'10" | 168.703 | -0.003 | 0.000009 |
| 168°42'15" | 168.704 | -0.002 | 0.000004 |
| 168°42'25" | 168.707 | +0.001 | 0.000001 |
| sums: | 674.822 | 0.000018 |
The computations aren't too onerous (a byproduct of using only three decimal places). However, once the angles are converted to decimal degrees, it's difficult to interpret magnitudes of subsequent calculations. Residuals are in decimal degrees; what are those in terms of the original mixed units? It's hard to judge if the residuals (and MPV, SD, EMPV) make sense for the measurement set.
(2) Convert to and carry seven decimal places
| Angle | Decimal Deg | v; deg | v2; deg2 |
| 168°42'30" | 168.7083333 | +0.0027777 | 0.0000077156 |
| 168°42'10" | 168.7027778 | -0.0027778 | 0.0000077162 |
| 168°42'15" | 168.7041667 | -0.0013889 | 0.0000019290 |
| 168°42'25" | 168.7069444 | +0.0013888 | 0.0000019288 |
| sums: | 674.8222222 | 0.0000192896 |
While the process is the same as the first, two things are readily apparent
- There are a lot more numbers to write down and uses in calculations
- The additional four decimal places have a significant impact the MPV, SD, and EMPV values.
Conclusion? Carrying only three decimal places results in substantial intermediate rounding. As we learned in the Significant Figures chapter, carrying more digits than needed and rounding at the end means less biased results.
But seven decimal places are sooooo many to carry. Would six be enough? Five? Four? We discussed how to convert angles to decimal degrees to the correct number of sig fig in the Significant Figures chapter. Although we could determine how many decimal places are needed, we still have the same issue as before: it's difficult to mentally compare decimal degree values to deg-min-sec.
But there's a better, simpler way
(3) Work with smallest unit
An angle is a mixed units quantity and usually, only the smallest unit changes, the others don't (more on that in a bit - be patient). Recognize a pattern: in our angles, each has 168° and 42'; only the seconds vary. We can simplify computations considerably if we work with just the seconds. To do that, subtract 168°42' (both of which are exact) from each angle.
| Angle | Sec only | v; sec | v2; sec2 |
| 168°42'30" | 30 | +10 | 100 |
| 168°42'10" | 10 | -10 | 100 |
| 168°42'15" | 15 | -5 | 25 |
| 168°42'25" | 25 | +5 | 25 |
| sums: | 80 | 250 |
Lookie there - the same exact results as carrying seven decimal places! And the computations are soooo much easier (you could almost do them all in your head). The residuals are in the smallest unit, seconds, so are easy to compare to their respective angle. We don't have to carry a lot of decimal places or figure out significant figures for the converted angles.
OK, but what about an angle set where the minutes vary? Let's use: 89°36'58", 89°36'55, 89°37'05', 89°37'10"
To work with only the seconds portion, subtract 89°36' from each angle. For the last two angles, the results are 01'05" and 01'10", respectively; write them as seconds: 65" and 70".
| Angle | Sec only | v; sec | v2; sec2 |
| 89°36'58" | 58 | -4.0 | +16.0 |
| 89°36'55" | 55 | -7.0 | +49.0 |
| 89°37'05" | 65 | +3.0 | +9.0 |
| 89°37'10" | 70 | +8.0 | +64.0 |
| sums: | 248 | 138.0 |
Could we have instead subtracted 89°37' from each angle? Sure:
| Angle | Sec only | v; sec | v2; sec2 |
| 89°36'58" | -02 | -02"-02.0" = -04.0" | +16.0 |
| 89°36'55" | -05 | -05"-02.0" = -07.0" | +49.0 |
| 89°37'05" | +05 | +05"-02.0" = +03.0" | +9.0 |
| 89°37'10" | +10 | +10"-02.0" = +08.0" | +64.0 |
| sums: | +08 | 138.0 |

The results are the same as before but this time we must keep track of negative numbers. It less error prone to subtract 89°36' instead of 89°37'.



