7. Error Propagation

Usually we combine measurements together to compute other quantities. Errors in those measurements affect the accuracy of the resulting computation. This is what’s meant by error propagation and it affects indirect measurements.

Because errors are plus-or-minus, they don't propagate in simple additive or multiplicative fashion. Remember that measurement analysis is based on statistics. A residual is the difference between a measurement and the best representation of the value; it's sorta like an error. In Equations F-2 and F-3 the residuals are squared, Equations F-2 through F-4 include the square root function. Combined errors typically propagate using squares and square roots. How those functions are incorporated depends on how measurements are combined. There are are many (infinite?) ways to combine measurements so there are many (infinite?) ways errors can propagate. Actually, with a little bit of calculus the propagation can be derived. 'Course, we're not here to learn calculus...

Three of the more common error propagations are Error of a Sum, Error of a Series, and Error of a Product.

a. Error of a Sum

This is the expected cumulative error when adding or subtracting measurements having individual errors.

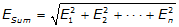	Equation F-5
ESum: Error of a sum Ei: Error of ith item

Example

A line is measured in three segments. The mean and error for each segment is shown in Figure F-4:

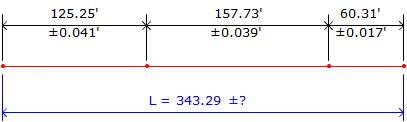Figure F-4 Error of a Sum: Addition

What is the error in the total length?

Substitute the individual errors into Equation F-5 and solve:

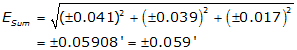
Why not just add up all three errors and use that as the error for the entire line?

0.041'+0.039'+0.017' = ±0.097'

That would assume all three errors behave identically. Since each is ±, what's to say the total isn't (+0.041-0.039-0.017) or (-0.041+0.039-0.017) or... As a matter of fact, the range for the first error is ±0.041: it can be anything between -0.041 and +0.041, ditto for the others.

The beauty of random errors...

How about if we subtract numbers which have errors? Well, basically the same thing.

Figure F-5 Error of a Sum: Subtraction

The error in the remaining length is:

Why not subtract the square of the errors instead of adding them? Consider if both segment errors were the same, for example, ±0.50'; subtracting the square of the errors means the remainder would have no error. Remember that each individual error is ± so they don't behave in a straight algebraic fashion.

b. Error of a Series

This is used when there are multiple occurrences of the same expected error. This is typical when measurements with similar errors are multiplied or divided.

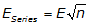Equation F-6

E is the consistent error

n is the number of times it occurs

Example

The interior angle sum of a five sided polygon, Figure F-6, is 540°00'00".

A survey crew is able to measure angles consistently to an accuracy of ±0°00’10.” (nearest second). How close to 540°00'00" should they expect to be after measuring all five angles?

Substitute into and solve Equation F-6:

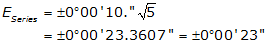
We would expect the crew’s angle sum to be within 00°00'23" of 540°00'00".

c. Error of a product

This is the expected error in the product of multiplied or divided numbers.

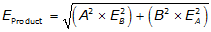Equation F-7

A, E_A are the measurement of a quantity and its error

B, E_B are the measurement of a second quantity and its error.

Notice that each product is the square of a quantity times the square of the error of the other quantity.

Example

The length and width of a parking lot are measured multiple times with the results shown in Figure F-7:

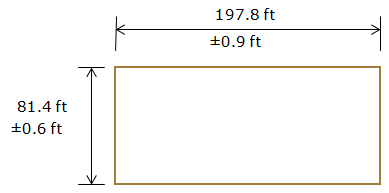Figure F-7 Error of a Product

The area of the parking lot is

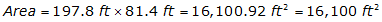
What is the error in that area? Substituting the dimensions and their errors in Equation F-7:

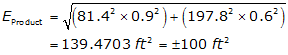
d. Others

There are many different types of error propagation depending how measurements are combined. Sometimes a sensitivity analysis, discussed earlier, is an easier way to estimate a final error. We’ll discuss error effects more as we look at different measurement and computational processes.

If you want to jump ahead you can check out random error propagation at these links: Chapter F. Electronic Distance Measurement and Chapter D. TSI Angle Error Sources and Behavior.