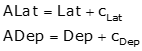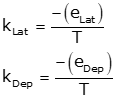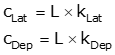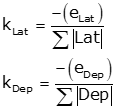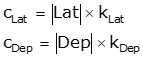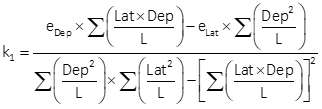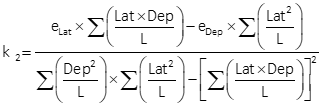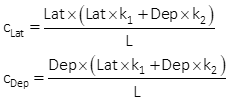K. Adjustment Methods Comparison
1. Introduction
Except for a pure least squares approach, the numeric adjustment methods described in Chapter E Section 1 are based on a general assumption of relative angle and distance accuracy.
The Transit Rule favors angles, the Crandall Method distances. The Compass Rule, the most common for simple traverses, treats angles and distances similarly.
This Chapter compares the three adjustment methods using a numerical example.
2. Common Nomenclature
| L | Length of a traverse side. |
| T | Total distance surveyed; sum of all side lengths |
| Lat, Dep | Latitude and departure of a side |
| eLat, eDep | Latitude and departure errors for the traverse |
| cLat, cDep | Latitude and departure correction for a side |
| ALat, ADep | Adjusted latitude and departure of a side |
The corrections for each method, while computed differently, are added to the unadjusted latitudes and departures, Equations K-1 and K-2.
|
|
Equations K-1 and K-2 |
3. Adjustment Equations Summary
a. Compass Rule
| kLat, kDep | Adjustment constants |
|
|
Equations K-3 and K-4 |
|
|
Equations K-5 and -6 |
b. Transit Rule
| kLat, kDep | Adjustment constants |
|
|
Equations K-7 and K-8 |
|
|
Equations K-9 and K-10 |
c. Crandall Method
Computations are a bit more involved because distances are adjusted by least squares. Topic XV. Least Squares Lite covers least squares adjustments in greater detail and ways to efficiently perform the complex computations which generally requires software. The equations presented here are based on those developed by Professor Crandall in the early 1900s, way before computers or even calculators (think slide rules). They are a relatively efficient way to manually perform the adjustment on a simple traverse.
| k1, k2 | Adjustment constants |
|
|
Equation K-11 |
|
|
Equation K-12 |
|
|
Equations K-13 and K-14 |
4. Example
a. Data
The traverse shown below will be adjusted by all three methods.
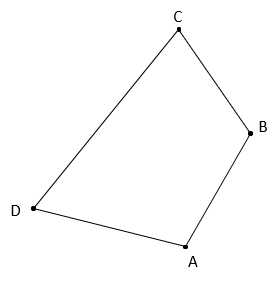
| Line | Azimuth | Length (ft) | Lat (ft) | Dep (ft) |
| AB | 30°00'00" | 365.79 | +316.783 | +182.895 |
| BC | 325°33'52" | 354.52 | +292.395 | -200.474 |
| CD | 219°03'25" | 645.84 | -501.508 | -406.939 |
| DA | 104°12'35" | 437.64 | -107.428 | +424.250 |
| sums: | 1083.79 | +0.242 | -0.268 |
The traverse misclosure is purposely large so adjustment differences are more easily seen.
For each adjustment
- Constants are computed
- Computations are shown for the first line
- Adjusted latitudes and departures are shown in a table along with adjusted lengths and directions
b. Compass Rule
Set up the adjustment constants using Equations K-3 and K-4.
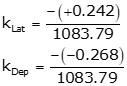
Adjust the latitude and longitude of each line using Equations K-5 and K-6. Computations for line AB are:
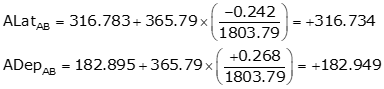
Fully adjusted traverse
| Line | ALat (ft) | ADep (ft) | Azimuth | Length (ft) |
| AB | +316.734 | +182.949 | 30°00'40" | 365.775 |
| BC | +292.347 | -200.421 | 325°34'02" | 354.451 |
| CD | -501.594 | -406.843 | 219°02'44" | 645.847 |
| DA | -107.487 | +424.315 | 104°12'54" | 437.717 |
| sums: | 0.000 | 0.000 |
c. Transit Rule
Set up the adjustment constants using Equations K-7 and K-8.

Adjust the latitude and longitude of each line using Equations K-9 and K-10. Computations for line BC are:
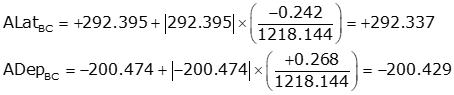
Fully adjusted traverse
| Line | ALat (ft) | ADep (ft) | Azimuth | Length (ft) |
| AB | +316.720 | +182.935 | 30°00'37" | 365.756 |
| BC | +292.337 | -200.429 | 325°33'54" | 354.447 |
| CD | -501.607 | -406.849 | 219°02'43" | 645.861 |
| DA | -107.450 | +424.343 | 104°12'34" | 437.736 |
| sums: | 0.000 | 0.000 |
d. Crandall Method
Set up the adjustment constants using Equations X-11 and -12.

Adjust the latitude and longitude of each line using Equations X-13 and -14. Computations for line AB are:
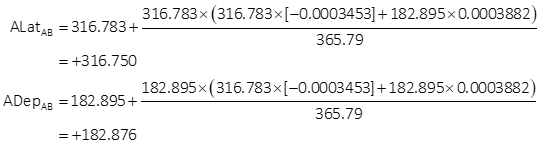
Fully adjusted traverse
| Line | ALat (ft) | ADep (ft) | Azimuth | Length (ft) |
| AB | +316.783 | +182.895 | 30°00'00" | 365.752 |
| BC | +292.395 | -200.474 | 325°33'52" | 354.341 |
| CD | -501.508 | -406.939 | 219°03'25" | 645.855 |
| DA | -107.488 | +424.250 | 104°12'35" | 437.842 |
| sums: | 0.000 | 0.000 |
e. Comparison of adjusted values
(1) Distances
| Line | Original | Compass | Transit | Crandall |
| AB | 365.79 | 365.756 | 365.756 | 365.752 |
| BC | 354.52 | 354.447 | 354.447 | 354.341 |
| CD | 645.84 | 645.861 | 645.861 | 645.855 |
| DA | 437.64 | 437.736 | 437.736 | 437.842 |
(2) Interior angles
| Point | Original | Compass | Transit | Crandall |
| A | 105°47'25" | 105°47'46" | 105°48'03" | 105°47'25" |
| B | 115°33'52" | 115°33'21" | 115°33'17" | 115°33'52" |
| C | 73°29'33" | 73°28'42" | 73°28'49" | 73°29'33" |
| D | 65°09'10" | 65°10'11" | 65°09'51" | 65°09'10" |
The Crandall Method puts all the corrections into distances so angles do not change from their original values. Because the Compass and Transit Rules modify the angles, they both also change the initial azimuth from 30°00'00"; the starting azimuth is unaffected with the Crandall Method.
If the initial direction must be held, then the direction of each line in the Compass and Transit Method adjustments should be rotated by a constant. The constant is the difference between the initial and adjusted directions of the first line. Even though rotating each line the same amount changes the latitudes and departures, traverse closure is not affected.
5. Summary
Of the three methods demonstrated here, the Compass Rule is the most commonly used for simple traverse adjustments. While the Crandall Method is a quasi-least squares approach, it's up to the user to decide how to deal with random angle errors. When traverses become more complex with cross-links, a true least squares adjustment is the best. See the XV. Least Squares Lite topic.
Traverse Adjustment is an Excel workbook which performs Compass, Transit, and Crandall Method adjustments on a loop traverse. It uses Visual Basic for Applications so be sure to have macros enabled.