4. Example
a. Data
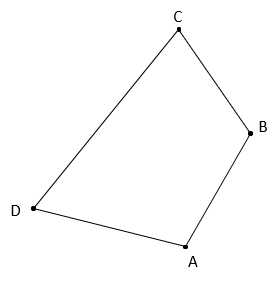
The traverse shown below will be adjusted by all three methods.
| Line | Azimuth | Length (ft) | Lat (ft) | Dep (ft) |
| AB | 30°00'00" | 365.79 | +316.783 | +182.895 |
| BC | 325°33'52" | 354.52 | +292.395 | -200.474 |
| CD | 219°03'25" | 645.84 | -501.508 | -406.939 |
| DA | 104°12'35" | 437.64 | -107.428 | +424.250 |
| sums: | 1083.79 | +0.242 | -0.268 |
The traverse misclosure is purposely large so adjustment differences are more easily seen.
For each adjustment
- Constants are computed
- Computations are shown for the first line
- Adjusted latitudes and departures are shown in a table along with adjusted lengths and directions
b. Compass Rule
Set up the adjustment constants using Equations K-3 and K-4.
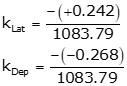
Adjust the latitude and longitude of each line using Equations K-5 and K-6. Computations for line AB are:
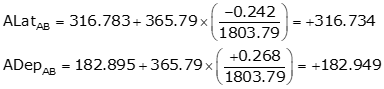
Fully adjusted traverse
| Line | ALat (ft) | ADep (ft) | Azimuth | Length (ft) |
| AB | +316.734 | +182.949 | 30°00'40" | 365.775 |
| BC | +292.347 | -200.421 | 325°34'02" | 354.451 |
| CD | -501.594 | -406.843 | 219°02'44" | 645.847 |
| DA | -107.487 | +424.315 | 104°12'54" | 437.717 |
| sums: | 0.000 | 0.000 |
c. Transit Rule
Set up the adjustment constants using Equations K-7 and K-8.

Adjust the latitude and longitude of each line using Equations K-9 and K-10. Computations for line BC are:
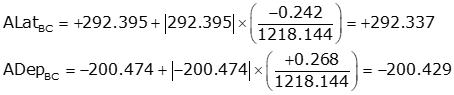
Fully adjusted traverse
| Line | ALat (ft) | ADep (ft) | Azimuth | Length (ft) |
| AB | +316.720 | +182.935 | 30°00'37" | 365.756 |
| BC | +292.337 | -200.429 | 325°33'54" | 354.447 |
| CD | -501.607 | -406.849 | 219°02'43" | 645.861 |
| DA | -107.450 | +424.343 | 104°12'34" | 437.736 |
| sums: | 0.000 | 0.000 |
d. Crandall Method
Set up the adjustment constants using Equations X-11 and -12.

Adjust the latitude and longitude of each line using Equations X-13 and -14. Computations for line AB are:
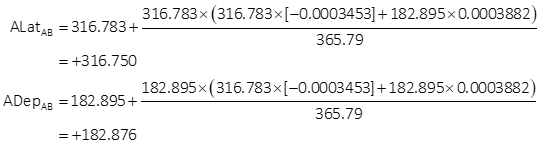
Fully adjusted traverse
| Line | ALat (ft) | ADep (ft) | Azimuth | Length (ft) |
| AB | +316.783 | +182.895 | 30°00'00" | 365.752 |
| BC | +292.395 | -200.474 | 325°33'52" | 354.341 |
| CD | -501.508 | -406.939 | 219°03'25" | 645.855 |
| DA | -107.488 | +424.250 | 104°12'35" | 437.842 |
| sums: | 0.000 | 0.000 |
e. Comparison of adjusted values
(1) Distances
| Line | Original | Compass | Transit | Crandall |
| AB | 365.79 | 365.756 | 365.756 | 365.752 |
| BC | 354.52 | 354.447 | 354.447 | 354.341 |
| CD | 645.84 | 645.861 | 645.861 | 645.855 |
| DA | 437.64 | 437.736 | 437.736 | 437.842 |
(2) Interior angles
| Point | Original | Compass | Transit | Crandall |
| A | 105°47'25" | 105°47'46" | 105°48'03" | 105°47'25" |
| B | 115°33'52" | 115°33'21" | 115°33'17" | 115°33'52" |
| C | 73°29'33" | 73°28'42" | 73°28'49" | 73°29'33" |
| D | 65°09'10" | 65°10'11" | 65°09'51" | 65°09'10" |
The Crandall Method puts all the corrections into distances so angles do not change from their original values. Because the Compass and Transit Rules modify the angles, they both also change the initial azimuth from 30°00'00"; the starting azimuth is unaffected with the Crandall Method.
If the initial direction must be held, then the direction of each line in the Compass and Transit Method adjustments should be rotated by a constant. The constant is the difference between the initial and adjusted directions of the first line. Even though rotating each line the same amount changes the latitudes and departures, traverse closure is not affected.